Markov Processes

April 20, 2025 · 8 min read · Page View:

If you have any questions, feel free to comment below. And if you think it's helpful to you, just click on the ads which can support this site. Thanks!

This is a summary of the lecture notes of Markov Processes.

Outline #

• Markov Process
• Brownian Motion
• Wiener Process
• Geometric Brownian Motion

Stochastic Process #

A stochastic process is defined by:

• A collection of time points (index $t$).
• The state space, which are the possible values of $X_t$, e.g.,${11,12,\cdots,16, 21, 22,\cdots, 26,\cdots, 61, 62,\cdots 66}$, or the price $S_t$ of a stock at day $t$.
• The simultaneous distribution of the variables $X_t$, including the distributions of all $X_t$ and their dependencies.

There are two important types of processes:

• Poisson process: All variables are identically and independently distributed. Examples include tossing a coin/die, queues for counters, call centers, servers, etc.
• Markov process: The variables are dependent in a simple manner.

Markov Process #

A 1st order Markov process in discrete time $(X_t),t = 1,\cdots$ satisfies the Markov Property:

In other words, only the present state determines the future state; the past is irrelevant. The Markov property does not imply independence between $X_{t - 1}$ and $X_{t+1}$. In fact, often $P(X_{t+1}=x_{t+1}|X_{t-1}=x_{t-1})$ are not zero.

M-ORDER MARKOV PROCESS #

A stochastic process $(X_t),t = 1,2,\cdots$ with the property:

Loosely speaking, the future depends on the most recent past $m$ states.

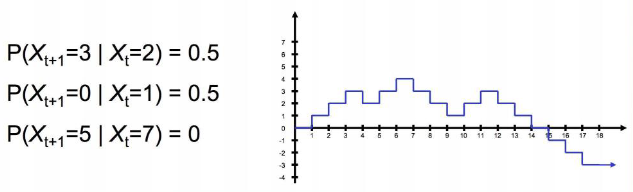
Transition Probabilities #

The transition probabilities are $P(X_{t+1}=x_{t + 1}|X_t=x_t)$ and $P(X_{t+1}=x_{t + 1}|X_s=x_s)$ for $s<t$.

Time Homogeneous Markov Process #

A Markov process is time homogeneous if the transition probabilities are independent of $t$:

eg. $P(X_{584}=5 |X_{583}=4)=P(X_{213}=5|X_{212}=4)$

For a time-homogeneous Markov process with $N$ states, the one-step transition matrix $P=[p_{ij}]$, where $1\leq i,j\leq N$ and $p_{ij}=P(X_{t+1}=x_j|X_t=x_i)$ is independent of $t$.

$x_i$ is the state.

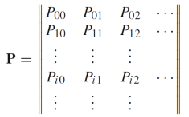
The initial distribution $(\pi_1,\cdots,\pi_N)$ gives the probabilities of the initial state, $\pi_i = P(X_1=x_i)$ for $i = 1,\cdots,N$ and $\sum_{i = 1}^{N}\pi_i=1$.

The $n$-step transition probabilities $p_{ij}^{(n)}=P(X_{t+n}=x_j|X_t=x_i)$.

Example: If

, then

and

eg. $p_{11}^{(2)} = p_{11}p_{11} + p_{12}p_{21}$ $= 0.35×0.35 + 0.65×0.81$ $= 0.1225 + 0.5265$ $= 0.6490$

We have known the start and end, then traverse(sum up) all possibilities in path.

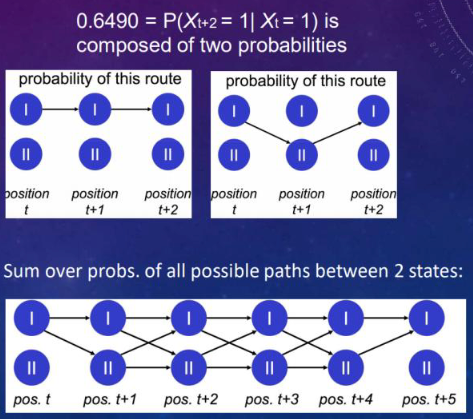
KOLMOGOROV-CHAPMAN EQUATION #

Let $P_{ij}$ be the one - step transition probabilities and $P_{ij}^n$ be the $n$-step transition probabilities. For all $n,m\geq0$ and $i,j = 1,\cdots,S$:

the probability that starting in state i the process will go to j in n + m transitions through a path which first takes it into state k at the nth transition,and then to state j in the next mth transition!

Wiener Process #

Consider a simple random walk ${X_N}$, where ${\xi_n}$ is a set of independent and identically distributed random variables with $P(\xi_k=\pm1)=\frac{1}{2}$. By the Central Limit Theorem, $\frac{X_N}{\sqrt{N}}\to N(0,1)$ in distribution.

Define a piecewise-constant random function $W_t^N=\frac{X_{\lfloor Nt\rfloor}}{\sqrt{N}}$ on $t\in[0,\infty)$.

As $N\to\infty$, $W^N$ converges in distribution to a stochastic process $W_t$ (or $W(t)$), which is the Wiener process.

A stochastic process $W(t)$ with values in $\mathbb{R}$ defined for $t\in[0,\infty)$ satisfies:

1. $W(0)=0$.
2. If $0<s<t$, then $W(t)-W(s)$ has a normal distribution $\sim N(0,t - s)$ with mean $0$ and variance $(t - s)$. :stationary
3. If $0\leq s<t\leq u<v$, then $W(t)-W(s)$ and $W(v)-W(u)$ are independent random variables. :Gaussianity
4. The sample paths $t\to W(t)$ are almost surely continuous.

In fact, the Wiener process is the only time-homogeneous stochastic process with independent increments that has continuous trajectories.

The probability density function of $W(t)$ is $f_{W(t)}(x)=\frac{1}{\sqrt{2\pi t}}e^{-\frac{x^2}{2t}}$.

Definition of Brownian Motion #

Brownian motion $B(t)$ is the unique process with the following properties:

1. No memory: $B_{t_1}-B_{t_0},B_{t_2}-B_{t_1},B_{t_3}-B_{t_2},\cdots$ are independent.
2. Invariance: The distribution of $B_{t + s}-B_s$ depends only on $t$.
3. Continuity.
4. $B_0 = 0$, $B_t - B_0 = B_t\sim N(0,t)$, $E(B_t)=0$, $Var(B_t)=t$.

Brownian motion is a Wiener process

Basic properties #

• Path regularity: $t\to B_t$ is continuous almost surely, but is nowhere differentiable almost surely. $dB(t)/dt \to \infty$
• $B_t$ is a Gaussian process. For all $0\leq t_1\leq\cdots\leq t_n$, the random vector $Z=(B_{t_1},\cdots,B_{t_n})$ has a multinormal distribution.
• $B_t$ has stationary increments: $(B_{t+h}-B_t)$ for $h>0$ has the same distribution for all $t$, $E(B_{t+h}-B_t)=0$ and $Var(B_{t+h}-B_t)=h$.
• Brownian motion is a martingale: $E(B_t|B_s)=B_s$ almost surely if $s<t$, where $F_s$ is the “information up to time $s$”. Which means, the expected value of $B_t$ at time $t$ is the value of $B_s$ at time $s$, the best prediction is now, which is related to the independent increments.
• $Cov(B_s,B_t)=\min(s,t)$

Local Extremes

• Brownian motion paths contain local maxima and minima in any non-trivial interval, making the set of local maxima and minima dense. This means that for any given number, there exists a local maximum or minimum arbitrarily close to it.
• Each local maximum and minimum is isolated, and the set of local maxima and minima is countable.

Increasing and Decreasing Points

• Define increasing and decreasing points: $\exists \epsilon > 0$ s.t. $\forall s \in (0, \epsilon)$, $f(t-s) \leq f(t) \leq f(t+s)$. Then $t$ is an increasing point (otherwise it is a decreasing point).
• But for standard Brownian motion, there are no pure increasing or decreasing points on any non-trivial interval. means the BM is not monotonic on any non-trivial interval.

Distributional Properties #

• Spatial Homogeneity: $B_t+x$ for any $x\in\mathbb{R}$ is a Brownian motion started at $x$.
• Symmetry: $-B_t$ is also a Brownian motion.
• Scaling: $cB_{\frac{t}{c^2}}$ for any $c>0$ is a Brownian motion.
• Time inversion: $Z_t=\begin{cases}0, & t = 0\tB_{\frac{1}{t}}, & t>0\end{cases}$
• Time reversibility: For any given $t>0$, ${B_s:0\leq s\leq t}\sim{B_{t - s}-B_t:0\leq s\leq t}$

Relatives of Brownian Motion #

• For $\mu\in\mathbb{R}$, $\sigma>0$, $x\in\mathbb{R}$, the process ${x+\mu t+\sigma W(t),t\geq0}$ is a Brownian motion with drift $\mu$ and diffusion coefficient $\sigma$ starting from $x$.
• For $Y_t = e^{x+\mu t+\sigma W(t)}$, the process $(Y_t,t\geq0)$ is a Geometric Brownian motion.
• For $B_t^0=W(t)-tW(1)$, the process $(B_t^0,t\geq0)$ is a Brownian bridge. normally used to model the stochastic process of fixed start and end.

Invariance Principle #

1. Random walk converges to Brownian motion: ${\sqrt{a}W_{\frac{t}{a}},t\geq0}\stackrel{a\to\infty}{\to}{B_t,t\geq0}$
2. Reflected random walk converges to reflected Brownian motion.

Why Brownian Motion? #

Brownian motion is unique:

• It is nowhere differentiable even though continuous everywhere.
• It is self-similar (fractal). The slices of BM also look like BM.
• It will eventually hit any real value. and return 0 again and again.
• It belongs to several families of stochastic processes, such as Markov processes, martingales, Gaussian processes, and Levy processes.

Brownian Motion for Financial Markets #

Financial markets (stock, foreign exchange, commodity, and bond markets) are often assumed to follow Brownian motion. A standard Brownian motion is insufficient for asset price movements and that a geometric Brownian motion is necessary.

Geometric Brownian Motion (GBM) #

Geometric Brownian Motion is the continuous-time stochastic process $X(t)=z_0e^{\mu t+\sigma W(t)}$, where $W(t)$ is a standard Brownian Motion. It is used as a simple model for market prices because it is always positive (with probability 1).

The relative change is given by $\frac{dX}{X}=\mu dt+\sigma dW$. A random variable $X$ has a log-normal distribution (with parameters $\mu$ and $\sigma$) if $\log(X)$ is normally distributed: $\log(X)\sim N(\mu,\sigma^2)$.

The probability density function of $X$ is:

At fixed time $t$, $GBM$ $X(t)=z_0e^{\mu t+\sigma W(t)}$ has a log - normal distribution with parameters $(\ln(z_0)+\mu t)$ and $\sigma\sqrt{t}$.

Reasonable Model for Stock Price-Geometric Brownian Motion #

The stock price $S$ can be modeled by $dS=\mu Sdt+\sigma Sdz$, where $\mu$ is the “expected return”, $\sigma$ is the “volatility”, and $Z$ is a Wiener process. Then $d\ln S=(\mu-\frac{\sigma^2}{2})dt+\sigma dz$.

The analytical solution $S = S_0e^{(\mu-\frac{\sigma^2}{2})t+\sigma Z}$.

$\ln S$ has $T$ - period changes that are normally distributed.

If $Z(t)$ is a Wiener process, for $dz\sim N(0, dt)$ = $N(0,1)\sqrt{dt}$ which $\Delta Z = Z(t+\Delta t)-Z(t)$:

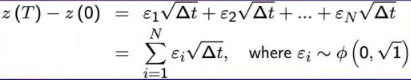
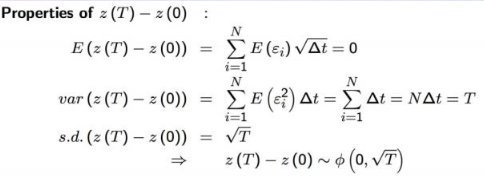
Some important things about WIENER PROCESS #

the Wiener process can be used to generate any continuous time stochastic process

Generalized Wiener Process $x$: a linear function of $z$ and time $dx =adt +bdz$, which $a dt$:deterministic component,or"drift"→$E(Ax)=at+bE(Az) =a t$,if $t=1$,then $E(△x)=a$!

For example, from time $0$ to $T$:

• $x(T)-x(0)=aT + b(z(T)-z(0))$ ,which is the change of $x$ in the time interval $[0, T]$.
• $E[x(T)-x(0)] = aT + bE[z(T)-z(0)] = aT$ ,the expected change of $x$ in the time interval $[0, T]$.
• $var[x(T)-x(0)] = b^{2}var[z(T)-z(0)] = b^{2}T$ ,the variance of the change of $x$ in the time interval $[0, T]$.
• $s.d.[x(T)-x(0)] = b\sqrt{T}$ ,the standard deviation of the change of $x$ in the time interval $[0, T]$.
• $x(T)-x(0)$ follows the normal distribution $N(aT,b\sqrt{T})$.

Consider the function $G(S,t)=\ln S$ , where $S$ is usually the stock price, and $t$ is time.

Ito’s Lemma provides a formula for differentiating a function of a stochastic process. For $dG = d\ln S$ , according to Ito’s Lemma formula $dG=\left(\frac{\partial G}{\partial S}\mu S+\frac{\partial G}{\partial t}+\frac{1}{2}\frac{\partial^{2}G}{\partial S^{2}}(\sigma S)^{2}\right)dt+\frac{\partial G}{\partial S}\sigma Sdz$ .

For $G(S,t)=\ln S$ , the partial derivatives are $\frac{\partial G}{\partial S}=\frac{1}{S}$ , $\frac{\partial G}{\partial t}=0$ , $\frac{\partial^{2}G}{\partial S^{2}}=-\frac{1}{S^{2}}$ . Substituting these partial derivatives into Ito’s Lemma formula:

$$ \begin{align*} dG&=\left[\frac{1}{S}\mu S + 0+\frac{1}{2}\left(-\frac{1}{S^{2}}\right)(\sigma S)^{2}\right]dt+\frac{1}{S}\sigma Sdz\\ &=\left(\mu-\frac{\sigma^{2}}{2}\right)dt+\sigma dz \end{align*} $$

So $\ln S$ is a generalized Wiener process. This conclusion makes it easier to analyze stock price-related analysis, as generalized Wiener processes have some good properties.

Stock Prices Are Log-Normally Distributed #

Since stocks follow the geometric brownian motion $dS=\mu Sdt+\sigma Sdz$, $\ln S$ follows the generalized Wiener Process $d\ln S=(\mu-\frac{\sigma^2}{2})dt+\sigma dz$. Assume $\mu\geq \sigma^2$, then:

or

Predicting Stock Prices with a GBM Model #

let $S_0$ is current stock price, $S_N$ is the stock price at future time $N$（$N=T/\Delta t$, if $\Delta t = 1$ means daily price）.

• daily return: $r_k=\frac{S_k - S_{k - 1}}{S_{k - 1}}$ （$k$ is time period）
• average return: $\hat{\mu}=\frac{1}{M}\sum_{k = 1}^{M}r_k$ calculate average to estimate $\mu$ and
• use $\hat{\sigma}=\sqrt{\frac{1}{M}\sum_{k = 1}^{M}(r_k-\hat{\mu})^2}$ to estimate $\sigma$ 。
• drift: $drift_k=\mu-\frac{\sigma^{2}}{2}$ which means long term deterministic trend
• diffusion: $diffusion_k=\sigma b_k= \sigma z_k$ and $b_k\sim N(0,1)$, which means short term random fluctuation
• stock price: $S_{t_1}=S_{t_0}+S_{t_0}drift_{t_1}+S_{t_0}diffusion_{t_1}$ $$ \begin{align*} S_{k}&=S_{k - 1} \cdot e^{(drift_{k}+diffusion_{k})}=S_{k - 1} \cdot e^{\left(\mu-\frac{1}{2}\sigma^{2}+\sigma z_{k}\right)}\\ S_{k}&=S_{0} \cdot e^{\left(\left(\mu-\frac{1}{2}\sigma^{2}\right)t_{k}+\sigma W_{k}\right)}\\ t_{k}&=k\\ W_{k}&=\sum_{i = 1}^{k}b_{i} \text{ and } b_{i}\sim N(0,1) \end{align*} $$

Related readings

• Stock Prices
• Possion Processes
• Stochastic Processes
• Random Walks
• Sequences of Random Variables