Random Walks

April 18, 2025 · 5 min read · Page View:

If you have any questions, feel free to comment below.

This article is a summary of the random walks in the book “Random Processes” by Gregory F. Lawler.

WHAT IS A RANDOM WALK #

A random walk is the process by which randomly-moving objects wander away from where they start.

The simplest random walk to understand is a 1-dimensional walk: Suppose that the black dot on the right is sitting on a number line and starts in the center. Then, it takes a step, either forward or backward, with equal probability. It keeps taking steps either forward or backward each time.
Let’s call the 1st step $a_1$, the second step $a_2$, the third step $a_3$ and so on.
- +1 (if the step is forward) with probabilities $p$
- -1 (if the step is backward) with probabilities $q = 1 - p$

The black dot that has taken 5 steps and ended up at -1 on the number line. Starting at 0, how far can it move in n steps?

$$ \pm S_{n}=a_{1}+a_{2}+a_{3}+\cdots+a_{n} $$

The sequence of Bernoulli trials $X_{1}, X_{2}, \cdots, X_n,\cdots$ with probability of success equal to $p$ in each trial, where $X_k = 1$ if the $k$th trial results in a success and $X_k=-1$ otherwise. Let $S_{n}=X_{1}+X_{2}+\cdots+X_{n}$ with $S_0 = 0$, the accumulated positive or negative excess at the $n$th trial. The particle takes a unit step up or down at regular intervals, and $S_n$ represents the position of the particle at the $n$-th step.

Examples #

In particles emitted and thermal noise.
Day-to-day stock prices are independent of each other, meaning that momentum does not generally exist and calculations of past earnings growth does not predict future growth. Securities prices are random and not influenced by past events.

Return to the origin (or zero) Problem in n successive steps #

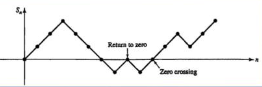
This is important as the process starts all over again from that point onward.

1st vs r-th return
Waiting time for 1/r-th return
Number of sign changes (zero crossings)
The level of maxima and minima and their corresponding probabilities

P{AT STAGE N, THE PARTICLE IS AT POINT R}:

$$ P\{S_n=r\}=\binom{n}{k}p^{k}q^{n - k} $$

where $k$ represents the number of successes in $n$ trials and $n-k$ the number of failures, so $r = k-(n - k)=2k - n$, then $k=\frac{n + r}{2}$, k must be the integer, so $n$ and $r$ must be even or odd together.

$$ p_{n,r}=\binom{n}{\frac{n + r}{2}}p^{\frac{n + r}{2}}q^{\frac{n - r}{2}} $$

RETURN TO ORIGIN #

Remember that $n$ and $r$ must be even or odd together!

$S_n = 0$ means the random walk has returned to the origin ($r = 0$ or $n = 2k\rightarrow n$ even). Probability of return at the $2n$th trial is $P{s_{2n}=0}=\binom{2n}{n}(pq)^{n}\triangleq u_{2n}$ with $u_0 = 1$

$$ \binom{\alpha}{k} = \frac{\alpha(\alpha - 1)(\alpha - 2)\cdots(\alpha - k + 1)}{k!} $$

The generalization of the binomial formula:

$$ (1 + x)^{\alpha}=\sum_{k = 0}^{\infty}\binom{\alpha}{k}x^{k} $$

By these formulas, we can transform $u_{2n}$ to $u_{2n}=(-1)^{n}\binom{-\frac{1}{2}}{n}(4pq)^{n}$

$$ \begin{aligned} u_{2n}&=\frac{(2n)!}{n!n!}(pq)^{n}\\ &=\frac{2n(2n - 2)\cdots4\cdot2}{n!}\cdot\frac{(2n - 1)(2n - 3)\cdots3\cdot1}{n!}(pq)^{n}\\ &=\frac{2^{n}n!}{n!}\cdot\frac{2^{n}(-1)^{n}(-\frac{1}{2})(-\frac{3}{2})\cdots(-\frac{1}{2}-(n - 1))}{n!}(pq)^{n}\\ &=(-1)^{n}\binom{-\frac{1}{2}}{n}(4pq)^{n} \end{aligned} $$

THE FIRST RETURN TO ORIGIN #

A first return to zero occurs at stage $2n$ if the event

$B_n={S_1\neq0,S_2\neq0,\cdots,S_{2n - 1}\neq0,S_{2n}=0}$.
Let $v_{2n}=P(B_n)=P{S_1\neq0,S_2\neq0,\cdots,S_{2n - 1}\neq0,S_{2n}=0}$, with $v_0 = 0$

$u_{2n}$ vs. $v_{2n}$: A visit to the origin at stage $2n$ is either the first return with probability $v_{2n}$ or the first return occurs at an earlier stage $2k < 2n$ with probability $v_{2k}$ followed by an independent new return to zero after $2n - 2k$ stages with probability $u_{2n - 2k}$ for $k = 1,2,\cdots,n$ As these events are mutually exclusive and exhaustive, we get the fundamental identity

$$ u_{2n}=v_{2n}+v_{2n - 2}u_{2}+\cdots+v_{2}u_{2n - 2}=\sum_{k = 1}^{n}v_{2k}u_{2n - 2k} $$

Moment generating function for $v_{2n}$:

$$ \begin{aligned} U(z)&=1+\sum_{n = 1}^{\infty}u_{2n}z^{2n}=1+\sum_{n = 1}^{\infty}(\sum_{k = 1}^{n}v_{2k}u_{2n - 2k})z^{2n}\\ &=1+\sum_{m = 0}^{\infty}u_{2m}z^{2m}\cdot\sum_{k = 0}^{\infty}v_{2k}z^{2k}=1+U(z)V(z)\\ &=\frac{1}{1 - V(z)} \end{aligned} $$$$ V(z)=\sum_{n = 0}^{\infty}v_{2n}z^{2n}=1-\frac{1}{U(z)}=1-\sqrt{1 - 4pqz^{2}} $$$$ V_{2n}=\frac{1}{2n - 1}\binom{2n - 1}{n}2(pq)^{n} $$

If one of the mutually exclusive events $B_1$ or $B_2,\cdots$ happens, then the particle will return to 0:

$$ \begin{aligned} P\{\text{particle will ever return to the origin}\}&=\sum_{n = 0}^{\infty}P(B_{n})\\ &=\sum_{n = 0}^{\infty}v_{2n}=V(1)=1-\sqrt{1 - 4pq}=1-|p - q|\\ &=\begin{cases}1-|p - q|<1&p\neq q\\1&p = q\end{cases} \end{aligned} $$

Thus if $p\neq q$, the probability that the particle will never return to the origin $P(S_{2k}<0),k\geq1)$ is $|p - q|\neq0$ and finite;
and if $p = q=\frac{1}{2}$, then with probability 1 the particle will return to the origin.

In a fair game ($p = q$) with infinite resources on both sides, sooner or later one should be able to recover all loss since return to the break-even point is bound to happen.

But how long would it take?

$(V_{2n})$ represents the probability distribution for the waiting time for the first return to origin. Its expected value

$$ \mu=V'(1)=\begin{cases}\frac{4pq}{|p - q|}&p\neq q\\\infty&p = q\end{cases} $$

As you can see, the expected waiting time is infinite if $p = q$.

LATER RETURNS TO THE ORIGIN #

Let $v_{2n}^{(r)}$ = the probability of $r$-th return to the origin at $2n$-th trial. As the trials following the first return to zero form a probabilistic replica of the whole sequence, so the $r$-th probability is related to the $(r-1)$-th probability.

$$ v_{2n}^{(r)}=\sum_{k = 0}^{n}v_{2k}v_{2n - 2k}^{(r - 1)} $$

The generating function of $v_{2n}^{(r)}$

$$ V^{(r)}(z)\triangleq\sum_{n = 0}^{\infty}v_{2n}^{(r)}z^{2n}=\sum_{k = 0}^{\infty}v_{2k}z^{2k}\sum_{m = 0}^{\infty}v_{2m}^{(r - 1)}z^{2m}=V(z)V^{(r - 1)}(z)=V^{r}(z) $$

And we know that:

$$ V^{r}(z)=2V^{r - 1}(z)-4pqz^{2}V^{r - 2}(z) $$

So we can get:

$$ v_{2n}^{(r)}=2v_{2n}^{(r - 1)}-4pqv_{2n - 2}^{(r - 2)} $$

Also by induction, $v_{2n}^{(r)}=\frac{r}{2n - r}\binom{2n - r}{n}2^{-(2n - r)}$ if $p = q=\frac{1}{2}$.

$$ \binom{n}{k}p^{k}q^{n - k}\simeq\frac{1}{\sqrt{2\pi npq}}e^{-(k - np)^{2}/2npq},p + q = 1 $$

When $r$ is also large, apply the De Moivre-Laplace theorem, and let $2n - r=m$, $k=\frac{m + r}{2}$, we can get the approximation: $r$-th return at the $m$-th trial.

$$ v_{m}^{(r)}=\sqrt{\frac{2}{\pi}}\frac{r}{m^{3/2}}e^{-r^{2}/2m} $$

while valid only if $m$ together with $r$ is either even or odd. For any $m = cr^{2}$, the probability that $r$ returns to origin occur before the instant $t = cr^{2}$

$$ \eta_{c}=\sum_{m = 0}^{cr^{2}}v_{m}^{(r)}=2\int_{1/\sqrt{c}}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-x^{2}/2}dx $$

Example: For $c = 10$, $\eta_{c}=0.7566$. In a fair game, to observe $r$ returns to zero with 75% confidence, one must be prepared to play $10r^{2}$ games.

The median for the total number of returns to zero is about $\frac{2}{3}\sqrt{N}$

Example: Simulation for 10,000 tosses of a fair coin in four separate trial runs. In a run of length 10,000 it is as likely that there occur fewer than 66 returns to zero.

WAITING TIME FOR A GAIN #

The event ${S_{1}\leq0,S_{2}\leq0,\cdots,S_{n - 1}\leq0,S_{n}=+1}$: the first visit to 1 or the first passage through +1.

Let $\phi_{n}=P(S_{1}\leq0,S_{2}\leq0,\cdots,S_{n - 1}\leq0,S_{n}=+1)$ with $\phi_{0}=0,\phi_{1}=p$.

For some $n>1$, then $S_{n}=-1$ with probability $q$: there must exist a smallest integer $k < n$ such that $S_{k}=0$, and it is followed by a new first passage through +1 in the remaining $(n - k)$ steps, $k = 1,2,\cdots,n - 2$

With $P(S_{1}=-1) = q$, $P(S_{1}=-1,S_{2}<0,\cdots,S_{k - 1}<0,S_{k}=0)=P(S_{1}=0,S_{2}<0,\cdots,S_{k - 1}<0,S_{k}=+1)=\phi_{k - 1}$, P(a new first passage through +1 in the remaining (n - k) steps) $=\phi_{n - k}$.

$$ \phi_{n}=q(\phi_{1}\phi_{n - 2}+\phi_{2}\phi_{n - 3}+\cdots+\phi_{n - 2}\phi_{1}) $$$$ \Phi(z)=\frac{1-\sqrt{1 - 4pqz^{2}}}{2qz} $$

Important:

$$ \phi_{2n - 1}=\frac{v_{2n}}{2q}=\frac{(-1)^{n - 1}}{2q}\binom{\frac{1}{2}}{n}(4pq)^{n};n\geq1 $$$$ \sum_{n = 1}^{\infty}\phi_{n}=\begin{cases}\frac{p}{q}&pExpected Waiting Time:

$$ \mu=\begin{cases}\frac{1}{p - q}&p>q\\\infty&p = q\\\frac{p}{q(q - p)}&q>p\end{cases} $$

FIRST PASSAGE THROUGH MAXIMA #

Let

$$ \phi^{(r)}_n = P\{\text{the first passage through }r>0\text{ occurs at the }n\text{th step}\} $$

r means the desired maximum gain. eg. $r=3$, $\phi^{(3)}_{10}$ means the probability that the first passage through 3 occurs at the 10th step.

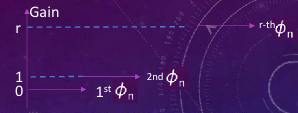
As the trials following the first passage through +1 form a replica of the whole sequence repeat itself, the waiting times between successive incremental first passages are independent, so that the waiting time for the first passage through a positive gain $r$ is the sum of $r$ independent random variables each with common distribution $\phi_{1}$. It means the $\phi^{(3)}$ is the sum of 3 independent random variables each with common distribution $\phi_{1}$. It was accumulated.

Moment Generating function:

$$ \Phi^{(r)}(z)\triangleq\sum_{n = 1}^{\infty}\phi_{n}^{(r)}z^{r}=\Phi^{r}(z) $$

It was accumulated conceptions.

$$ \phi_{m}^{(r)}=\frac{r}{m}\binom{m}{\frac{m + r}{2}}p^{\frac{m + r}{2}}q^{\frac{m - r}{2}} $$

When $p = q=\frac{1}{2}$, $P{\text{1st passage through }r\text{ at the }n\text{-th stage}}=\frac{r}{n}\binom{n}{\frac{n + r}{2}}2^{-n}$

For $n = cr^{2}$, the probability that the first passage through gain $r$ occurs before the instant $t = cr^{2}$

$$ \sum_{n = 0}^{N}\phi_{n}^{(r)}\simeq\frac{1}{2}\int_{0}^{cr^{2}}\sqrt{\frac{2}{\pi}}\frac{r}{n^{3/2}}e^{-r^{2}/2n}dn=2\int_{1/\sqrt{c}}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-x^{2}/2}dx $$

The random walk problem - drunken sailor walk #

Review of the formula #

The problem: There is a drunk man coming out of a pub. He cannot control his steps, and randomly (with 1/2 probability makes a step forward and backward, Let us assume that the length of his steps is fixed(1m). Determine the probability, that after N steps he is at a distance L from the starting point.

total number of tracks: $2^N$, the probability to follow one given track is $P=(1/2)^{N}$

The number of tracks with N steps that are finishing at coordinate x:

possible values of x:${N, N-2, N-4…..-(N-2), -N}$

let $N_+$ be the number of steps in + direction; ${N_-}$ the number of steps in- direction

$N_+ + N_- = N$
$x = N_+ - N_-$

Hence:

$N_+ = (N + x) / 2$
$N_- = (N - x) / 2$

So we can calculate the number of tracks with N steps that are finishing at coordinate x:

$$ W(N,x)=\frac{N!}{(\frac{N + x}{2})!(\frac{N - x}{2})!} $$

The true probability to be at a distance L from the starting point after N steps is:

$$ P(N,x)=\frac{W(N,x)}{2^N}=\frac{N!}{(\frac{N + x}{2})!(\frac{N - x}{2})!}\frac{1}{2^N} $$

Stirling’s approximation #

But the factorial is very large, it’s hard to calculate. So we will use Stirling’s approximation:

$$ \ln(N!)\cong N\ln(N)-N+\frac{1}{2}\ln(2\pi N) $$

Meanwhile, put the ln into the true formula:

$$ \ln [P(N, x)]=-\frac{1}{2} \ln (2 \pi N)+\ln (2)-\left(\frac{N+x+1}{2}\right) \ln \left(1+\frac{x}{N}\right)-\left(\frac{N-x-1}{2}\right) \ln \left(1-\frac{x}{N}\right) $$

And when the N » 1 as well as $x/N « 1$, we can approximate:

$$ \ln\left(1\pm\frac{x}{N}\right)\approx\pm\frac{x}{N}-\frac{1}{2}\left(\frac{x}{N}\right)^2 $$

So we can simplify the formula:

$$ \ln[P(N,x)]\approx -\frac{1}{2}\ln(2\pi N)+\ln(2)-\frac{x^{2}}{2N} $$

In the end, the approximate formula is:

$$ P(N,x)=\sqrt{\frac{2}{\pi N}}e^{-\frac{x^{2}}{2N}} $$

And its integral is:

$$ \int_{-\infty}^{\infty}P(N,x)dx=2 $$

The expected value of x(<x>) is:

Normal approximation #

This random walk process can be regarded as N independent Bernoulli trials, which conforms to the binomial distribution $X\sim B(N,\frac{1}{2})$. When N is large and p is fixed(condition), according to the central limit theorem, the binomial distribution $X\sim B(N,p)$ approximately follows the normal distribution $N(np,np(1 - p))$. In this problem, $p = \frac{1}{2}$, so it approximately follows the normal distribution $N(\frac{N}{2},\frac{N}{4})$.

For the normal distribution $N(\mu,\sigma^{2})$, the probability density function is $f(x)=\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(x - \mu)^{2}}{2\sigma^{2}}}$. Substituting $\mu=\frac{N}{2}$ and $\sigma^{2}=\frac{N}{4}$, we can obtain:

$$ P(N,x)\approx\frac{1}{\sqrt{2\pi\times\frac{N}{4}}}e^{-\frac{(x-\frac{N}{2})^{2}}{2\times\frac{N}{4}}}=\sqrt{\frac{2}{\pi N}}e^{-\frac{(x - \frac{N}{2})^{2}}{\frac{N}{2}}} $$

So the result is same as the result of Stirling’s approximation, so we combine them in the one formula.

Possion approximation #

In this random walk problem, it is not appropriate to directly use the Poisson approximation to solve it.

The Poisson distribution is suitable for describing the number of rare events occurring within a fixed time or space. Its application conditions usually require that

the probability p of an event occurring is very small (generally p -> 0)
the number of trials n is large (n -> $\infin$)
$\lambda = np$ is moderate and fixed number.

However, in the scenario of this random walk, the probability $p=\frac{1}{2}$ for each step forward or backward, which does not meet the condition that p is very small. If the Poisson approximation is forced to be used, it will lead to relatively large errors, and it is impossible to accurately obtain the probability of being at a distance L after N steps. This is because the characteristics of the Poisson distribution differ greatly from the equal probability step length movement pattern in the random walk, and it cannot well fit the probability distribution of this problem.

Although this scenario is not suitable, I can still try it. Suppose we consider the number of times moving right within a certain number of steps as a random variable $Y$. In the original random walk, the probability of moving right is $p = \frac{1}{2}$, and the probability of moving left is $1 - p=\frac{1}{2}$. If we want to use the Poisson distribution for approximation, the number of times $Y$ moving right in an $N$-step random walk can be approximated as a Poisson distribution.

The probability formula for the Poisson distribution is $P(X = k)=\frac{e^{-\lambda}\lambda^{k}}{k!}$, let $\lambda=\frac{N}{2}$ (because the expected number of steps moving right is $N\times\frac{1}{2}$).

Let the number of steps moving right be $k$, and the number of steps moving left be $N - k$. The final position $x = k-(N - k)=2k - N$, then $k=\frac{N + x}{2}$.

So the probability estimated using the Poisson distribution is:

$$ P(N,x)=\frac{e^{-\frac{N}{2}}(\frac{N}{2})^{\frac{N + x}{2}}}{(\frac{N + x}{2})!} $$

Interesting examples #

Cliff of Doom and Pit of Disaster #

Gambling strategy #

A gambler goes to Las Vegas with $n$ in her pocket. Her plan is to make only $1 bets and somehow she has found a casino that will offer her truly even odds¹; namely, she will win or lose $1 on each bet with probability 1/2. She’ll play until she is broke or she has won $m$. In the latter case, she will go home with

$$w = n + m$$

dollars. What’s the probability that she goes home a winner?

The gambler goes home broke with probability

$$\frac{n}{w}=\frac{m}{n + m}$$

the gambler goes home a winner with probability

$$\frac{w - n}{w}=\frac{n}{n + m}$$

the gambler goes home with probability

$$\frac{n}{n + m}+\frac{m}{n + m}=1$$

and the number of bets before the gambler goes home is expected to be

$$n(w - n)=nm$$

If the gambler gets greedy and keeps playing until she goes broke, then

the gambler eventually goes broke with probability 1, and
the number of bets before the gambler goes broke is expected to be infinite.