Repeated Trials

February 28, 2025 · 5 min read · Page View:

If you have any questions, feel free to comment below.

This article is mainly about Bernoulli Trials and its properties.

If you lack the basic knowledge of probability, you can read the Probability and its Axioms first.

Independent Events #

Independent: Event A and B are independent if P(AB) = P(A)P(B)

More generally, a family of events $A_1, A_2, \cdots, A_n$ are independent if for any subset $A_{i_1}, A_{i_2}, \cdots, A_{i_k}$ of these events,

$$ P\left(\bigcap_{k=1}^{n} A_{i_{k}}\right)=\prod_{k=1}^{n} P\left(A_{i_{k}}\right) . $$

Independent events obviously cannot be mutually exclusive. eg, flipping a coin twice, the result of the second flip is independent of the first flip. Only the head or tail of once flip can be mutually exclusive.

Let $A=A_{1} \cup A_{2} \cup A_{3} \cup \cdots \cup A_{n}$, a union of n independent events.

$$ P(\overline{A}) = P(\overline{A_1}\overline{A_2}\cdots\overline{A_n}) = \prod_{i = 1}^{n}P(\overline{A_i}) = \prod_{i = 1}^{n}(1 - P(A_i)) $$

Thus for any such A $P(A)=1-P(\overline{A})=1-\prod_{i=1}^{n}\left(1-P\left(A_{i}\right)\right)$

eg. Example: Three switches connected in parallel operate independently. Each switch remains closed with probability p.

(a) Find the probability of receiving an input signal at the output.

(b) Find the probability that switch S is open given that an input signal is received at the output.

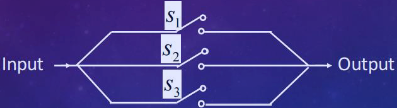
a. Let $A_i$ be the event that switch $S_i$ is closed. Then $P(A_i) = p$. The event that an input signal is received at the output is $A = A_1 \cup A_2 \cup A_3$.

$$ P(A) = 1 - P(\overline{A}) = 1 - \prod_{i=1}^{3}(1 - P(A_i)) = 1 - (1 - p)^3 $$

b. We want to find $P(\overline{A_1}|R)$.

From Bayes’ theorem,

$$ P(\overline{A_1} | R)=\frac{P(R | \overline{A_1}) P(\overline{A_1})}{P(R)}=\frac{(2 p - p^{2})(1 - p)}{3 p - 3 p^{2}+p^{3}}=\frac{2 - 2 p + p^{2}}{3 p - 3 p^{2}+p^{3}} $$

Because of the symmetry of the switches, we also have

$$ P(\overline{A_1} | R) = P(\overline{A_2} | R) = P(\overline{A_3} | R) $$

Cartesian Products #

If A is a subset of S1 and B is a subset of S2, then $C=A\times B$ is the set of all pairs $(e_1,e_2)$, where $e_1\in A$ and $e_2\in B$.

$$ A\times B=(A\times S2)\cup(B\times S1) $$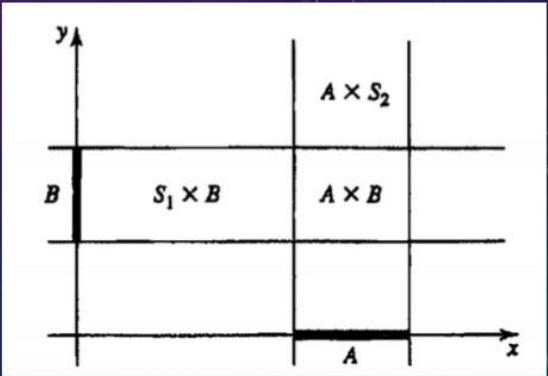

eg. Example 1-3: A box $B_1$ contains 10 white and 5 red balls and a box $B_2$ contains 20 white and 20 red balls.

A ball is drawn from each box. What is the probability that the ball from $B_1$ will be white and the ball from $B_2$ red?

Let $S_1$ be the experiment that the ball from $B_1$, $W_1$ is white and $S_2$ be the experiment that the ball from $B_2$, $R_2$ is red.

$$ P(W_1 \times R_2) = P(W_1)P(R_2) = \frac{10}{15}\times\frac{20}{40} = \frac{1}{3} $$

Assuming the two experiments are independent.

Bernoulli Trials #

Solution: Let $(\Omega,F,P)$ be the probability model for a single trial. The outcome of $n$ experiments is an $n$-tuple $\omega={\xi_{1}, \xi_{2}, \cdots, \xi_{n}} \in \Omega_{0}$

The probability of occurrence of such an o is given by

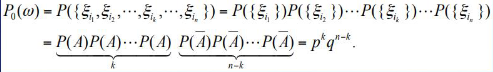
Recall that, starting with n possible choices, the first object can be chosen n different ways, and for every such choice the second one in n-1 ways,..and the kth one n-k+1 ways, and this gives the total choices for k objects out of n to be

$$ N=\frac{n(n-1) \cdots(n-k+1)}{k !}=\frac{n !}{(n-k) ! k !}=\binom{n}{k} $$

the number of combinations, or choices of n identical objects taken k at a time.

Independent repeated experiments, where the outcome is either a “‘success” or a “failure” are characterized as Bernoulli trials, and the probability of k successes in n trials is given by

$$ P_{n}(k)=P(A\text{ occurs exactly }k\text{ times in }n\text{ trials})=\binom{n}{k}p^{k}q^{n - k},\quad k = 0,1,2,\cdots,n $$

where p represents the probability of “‘success” in any one trial.

Let $X_k$ = exactly k successes in n trials.

Thus $$ P\left(X_{0} \cup X_{1} \cup \cdots \cup X_{n}\right)=\sum_{k=0}^{n} P\left(X_{k}\right)=\sum_{k=0}^{n}\binom{n}{k} p^{k} q^{n-k} . $$

Solution: With (X_{i}, i=0,1,2, \cdots, n,) 一 “exactly k occurrences of A in n trials”,mutually exclusive events. Thus

$$ P(\text{Occurrences of A is between } k_{1} \text{ and } k_{2} ) = \sum_{k=k_{1}}^{k_{2}} P\left(X_{k}\right)=\sum_{k=k_{1}}^{k_{2}} \binom{n}{k} p^{k} q^{n-k} . $$

eg. players A and B agree to play a series of games on the condition that A wins the series if he succeeds in winning m games before B wins n games. The probability of winning a single game is p for A and q=1-p for B.

Let PA= Prob (A wins m games before B wins n games), PB= Prob(B wins n games before A wins m games

By the (m+n-1) games,one wins PA+PB=1

Let $X_k =$ {A wins m games in exactly m+k games}, $k = 0,1,2,\cdots,n-1$ M.E.

Thus (A wins)=$X_0 \cup X_1 \cup \cdots \cup X_{n-1}$

$P(A \text{ wins}) = P(X_0 \cup X_1 \cup \cdots \cup X_{n-1}) = \sum_{k=0}^{n-1} P(X_k)$

So once A wins, he must win the last game and m-1 games in the first m+k-1 games. Thus we can list the following:

P(A wins m-1 games in any order among the first m+k-1 games) * P(A win the last game)

$$ P(X_k) = (\frac{m+k-1}{m-1}) p^{m-1} q^{k} * p $$

The properties of $P_n(k)$ #

$P_n(k) = \binom{n}{k} p^k q^{n-k}$
$\sum_{k=0}^{n} P_n(k) = 1$
$P_n(k) = P_n(n-k)$

$P_n(k)$ is a function of k increases until k=(n+1)p

As k increases, P(k) increases reaching a maximum (max) where

$$ (n+1) p-1 \leq k_{max } \leq(n+1) p $$

If k is not an integer, the maximum $P_n(k)$ occurs at the largest integer less than k.
If k is an integer, the maximum $P_n(k)$ occurs at k and k-1.

The most likely number of successes in n trials, (max) satisfies

$$ p-\frac{q}{n} \leq \frac{k_{max }}{n} \leq p+\frac{p}{n}, $$

$$ lim_{n \to \infty} \frac{k_{m}}{n}=p $$

Bernoulli Theorem #

Let A denote an event whose probability of occurrence in a single trial is p. If k denotes the number of occurrences of A in n independent trials.

The frequency definition of probability of an event (k/n) and its axiomatic definition (p) can be made compatible to any degree of accuracy.

$$ P({|\frac{k}{n}-p|>\varepsilon})<\frac{pq}{n\varepsilon^{2}} $$

Some ideas: for a given (\varepsilon), the probability of (|\frac{k}{n}-p|>\varepsilon) decreases as n increases. When the n is very large, we can make the fractional occurrence (relative frequency) (k/n) as close to the actual probability p of the event A in a single trial. Since k max is the most likely number of occurrences of A in n trials, as n increasing to infinity, the p tends to around k max.