Two Random Variables

February 1, 2025 · 0 min read · Page View:

Tutorial

Random Process | Math

If you have any questions, feel free to comment below.

This article is about the two random variables and their properties.

Two r.v. X, Y and Properties of their Distributions #

$$ P(x_{1} Joint Probability #

Joint Probability: The likelihood of two events occurring together and at the same time.

Towards this, we define the joint probabilit distribution function of X and Y to be

$$ F_{X Y}(x, y) =P[(X(\xi) \leq x) \cap(Y(\xi) \leq y)] =P(X \leq x, Y \leq y) \geq 0, $$

where x and y are arbitrary real numbers.

Some properties #

Since

$$ F_{X Y}(-\infty, y)=F_{X Y}(x,-\infty)=0, F_{X Y}(+\infty,+\infty)=1 . F_{X Y}(-\infty, y) \leq P(X(\xi) \leq-\infty)=0 . $$

we get

$$ (X(\xi) \leq+\infty, Y(\xi) \leq+\infty)=\Omega, F_{X Y}(\infty, \infty)=P(\Omega)=1 . $$

So:

$$ P\left(X(\xi) \leq x, y_{1}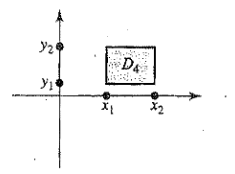

$$ P\left(x_{1}By definition, the joint p.d.f of X and Y is given by

$$ f_{X Y}(x, y)=\frac{\partial^{2} F_{X Y}(x, y)}{\partial x \partial y} . $$

Marginal Statistics #

$$ F_{X}(x)=P(X \leq x)=P(X \leq x, Y \leq \infty)=F_{X Y}(x,+\infty) . $$

Therefore

$$ F_{X}(x)=F_{X Y}(x,+\infty), F_{Y}(y)=F_{X Y}(+\infty, y) . $$

Thus

$$ F_{X}(x)=F_{X Y}(x,+\infty)=\int_{-\infty}^{x} \int_{-\infty}^{+\infty} f_{X Y}(u, y) d u d y $$

and taking derivative with respect to x, we get

$$ f_{X}(x)=\int_{-\infty}^{+\infty} f_{X Y}(x, y) d y, f_{Y}(y)=\int_{-\infty}^{+\infty} f_{X Y}(x, y) d x . $$

Differentiation rules #

$$ H(x)=\int_{a(x)}^{b(x)} h(x, y) d y . $$

Then

$$ \frac{d H(x)}{d x}=\frac{d b(x)}{d x} h(x, b)-\frac{d a(x)}{d x} h(x, a)+\int_{a(x)}^{b(x)} \frac{\partial h(x, y)}{\partial x} d y . $$

Joint probability mass function PMF #

$$ P\left(X=x_{i}\right)=\sum_{j} P\left(X=x_{i}, Y=y_{j}\right)=\sum_{j} p_{i j} $$$$ P\left(Y=y_{j}\right)=\sum_{i} P\left(X=x_{i}, Y=y_{j}\right)=\sum_{i} p_{i j} $$

Example 7.1: Given

$$ f_{X Y}(x, y)=\left\{\begin{array}{cc} constant, & 0 Obtain the marginal p.d.fs $fx(x)$ and $f_{Y}(y) .$

note: knowing the marginal pdf alone does not tell us everything about the joint pdf. Unless they are statistically independent.

Independence #

If the r.v X and Y are independent, then

$$ P((X(\xi) \leq x) \cap(Y(\xi) \leq y))=P(X(\xi) \leq x) P(Y(\xi) \leq y) $$$$ F_{X Y}(x, y)=F_{X}(x) F_{Y}(y) $$$$ f_{X Y}(x, y)=f_{X}(x) f_{Y}(y) $$$$ P_{X|Y}(x|y)=P_{X}(x) $$

eg. Example 7.3: Given

$$ f_{X Y}(x, y)= \begin{cases} x y^{2} e^{-y}, & 0for $\int_{0}^{\infty} y^{2}e^{-y}dy$ using integration by parts

integration by parts formula:

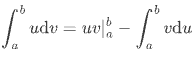
let $u = y^{2}$，$\mathrm{d}v = e^{-y}\mathrm{d}y$
for $u$ we can get $\mathrm{d}u = 2y\mathrm{d}y$，for $\mathrm{d}v$ we can get $v = -e^{-y}$
according to the integration by parts formula:

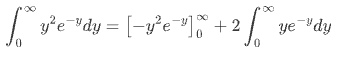
calculate $\left[-y^{2}e^{-y}\right]_{0}^{\infty}$:

when $y \to \infty$，the exponential function $e^{-y}$ tends to $0$ faster than any polynomial function tends to $\infty$，so $\lim_{y \to \infty}-y^{2}e^{-y} = 0$

when $y = 0$，$-y^{2}e^{-y} = 0$，therefore $\left[-y^{2}e^{-y}\right]_{0}^{\infty}= 0 - 0 = 0$.

for $\int_{0}^{\infty} ye^{-y}dy$ using integration by parts again.

One function of Two r.v.s #

Form a new r.v. Z by a function of X and Y:

$$ Z = g(X, Y) $$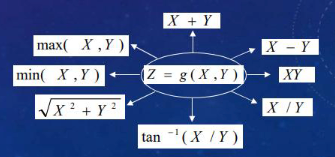

Given the joint p.d.f of X and Y $f_{X Y}(x, y)$, we can find the p.d.f of Z by:

$$ \begin{aligned} F_{Z}(z) & =P(Z(\xi) \leq z)=P(g(X, Y) \leq z)=P\left[(X, Y) \in D_{z}\right] \\ =\iint_{x, y \in D_{z}} f_{X Y}(x, y) d x d y, \end{aligned} $$

X+Y, X-Y #

eg Z = X + Y find $f_{Z}(z)$

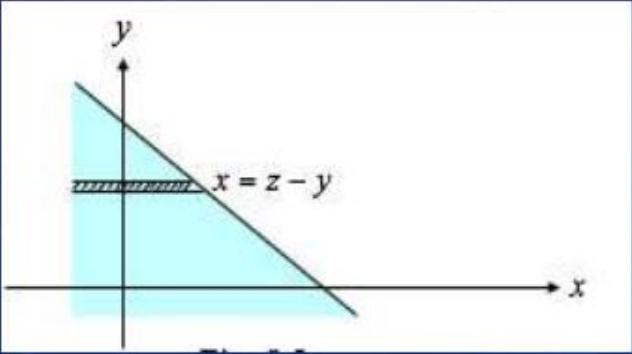
$$ F_Z(z)=P(X + Y\leq z)=\int_{y = -\infty}^{+\infty}\int_{x = -\infty}^{z - y}f_{XY}(x,y)dxdy $$$$ H(z)=\int_{a(z)}^{b(z)} h(x, z) d x. $$

Then

$$ \frac{d H(z)}{d z}=\frac{d b(z)}{d z} h(b(z), z)-\frac{d a(z)}{d z} h(a(z), z)+\int_{a(z)}^{b(z)} \frac{\partial h(x, z)}{\partial z} d x . $$

Thus

$$ f_{Z}(z) & =\int_{-\infty}^{+\infty}\left(\frac{\partial}{\partial z} \int_{-\infty}^{z-y} f_{X Y}(x, y) d x\right) d y=\int_{-\infty}^{+\infty}\left(f_{X Y}(z-y, y)-0+\int_{-\infty}^{z-y} \frac{\partial f_{X Y}(x, y)}{\partial z}\right) d y \\ & =\int_{-\infty}^{+\infty} f_{X Y}(z-y, y) d y . $$

Special case:

$$ f_{X}(x)=0, x<0, and f_{Y}(y)=0, y<0. $$$$ F_{Z}(z)=\int_{y=0}^{z} \int_{x=0}^{z-y} f_{X Y}(x, y) d x d y $$$$ f_{Z}(z)=\int_{y=0}^{z}\left(\frac{\partial}{\partial z} \int_{x=0}^{z-y} f_{X Y}(x, y) d x\right) d y=\left\{\begin{array}{cc} \int_{0}^{z} f_{X Y}(z-y, y) d y, & z>0, \\ 0, & z \leq 0 . \end{array}\right. $$

XY, X/Y #

X2 + Y2 , √(X2 + Y2) #

Max/Min(X, Y) #

Two functions of two r.v.s #

Given two functions $g(x,y)$ and $h(x,y)$, define the new random variables $Z=g(X, Y)$ $W=h(X, Y) .$

How to determine the joint p.d.f of $f_{ZW}(z,w)$?

For given z and w,

$$ \begin{aligned} F_{Z W}(z, w) & =P(Z(\xi) \leq z, W(\xi) \leq w)=P(g(X, Y) \leq z, h(X, Y) \leq w) =P\left((X, Y) \in D_{z, w}\right)=\iint_{(x, y) \in D_{t, w}} f_{X Y}(x, y) d x d y, \end{aligned} $$

where $D_{s, w}$ is the region in the xy plane such that the inequalities $g(x,y) \leq z$ and $h(x,y) \leq w$ are simultaneously satisfied.